Planeamento da construção
Esta página contém uma versão de trabalho de um ou mais textos. Estes devem ser lidos enquanto tal.
Considerações Gerais
Conceitos Chave
Listas de tarefas
Work Breakdown Structure (WBS)
Sistemas de Classificação de Informação para a Construção
Encadeamento de tarefas
O encadeamento de tarefas depende de condicionantes de diferentes tipos:
- físicas – por exemplo, para rebocar é necessário ter realizado a parede
- de recursos – a possibilidade de realizar uma tarefa pode ter restrições de meios, apesar das outras condições estarem reunidas, por exemplo, limitação de jogos de cofragem em obras de estruturas
- de segurança – obrigatoriedade de respeitar determinados prazos, por exemplo, prazos de cura em obras de estruturas
- programáticas – resultantes não de imposições técnicas, mas de programa (Dono de Obra, Caderno de Encargos, etc.)
As relações de encadeamento entre actividades podem ser de vários tipos:
- Fim-Início
- Início-Início
Noa: O início de “B” depende da realização total ou parcial de “A”. Pode ser transformada numa relação fim-início por decomposição de “A”.
- Fim-Fim
Nota: O fim de “B” depende do fim total ou parcial de “A”. Pode ser transformada numa relação fim início por decomposição de “B”.
- Início-Fim
O fim de “B” depende do início de “A”. Esta relação é difícil de evidenciar na prática.
Durações e recursos necessários
-
Margens
Margem Total
Atraso permitido a uma actividade sem que implique atrasos na conclusão do projecto (embora possa comprometer as datas de início mais cedo)
MT = DFMT (x) – DIMC (x) – t
Margem Livre
Atraso máximo que a tarefa pode ter sem que impeça o início mais cedo das sucessoras
ML = menor DIMC (x+i) – DIMC (x) – t
Margem Independente
Atraso máximo de uma actividade, sem impedir o arranque das suas sucessoras na DIMC nem a conclusão das antecessoras nas DFMT.
MI = Menor DIMC (x+i) – Maior DFMT (x-i) – t
- (x+i): actividades imediatamente sucessoras de x
- (x-i): actividades imediatamente antecessoras de x
Caminho Crítico
Sequência de actividades, do início até ao fim, em que as margens total, livre e independente são nulas (ML = MT = MI = 0).
O atraso nestas actividades compromete a data de conclusão do projecto.
Métodos
"Tradicionais"
As redes CPM e os diagramas de Gantt são métodos tradicionalmente aplicados ao planeamento. Podem ser calculados por processos manuais, embora actualmente sejam mais frequentemente obtidos através do uso de ferramentas informáticas. Em ambos os casos, as durações das tarefas a considerar são definidas de forma determinística. A utilização de redes PERT (Program Evaluation and Review Technique) permite introduzir incerteza na duração das tarefas.
Diagramas de Gantt
Um diagrama de Gantt permite associar as tarefas a uma escala de tempos.
Este método permite uma leitura fácil das durações das tarefas e do seu encadeamento. A representação gráfica das tarefas permite reconhecer relações de precedência entre tarefas e prazos de execução previstos com uma necessidade mínima de anotações complementares. A realização de balizamentos é, também, simples.
Por outro lado, a aplicação manual deste método a projectos com muitas tarefas torna-se difícil e morosa. Nestes casos, poderá não ser simples o cálculo de margens de tarefas nem a determinação de um caminho crítico.
Este tipo de diagrama é essencialmente destinado a leitura, não a cálculo excepto para projectos muito simples, com um pequeno número de tarefas.
Redes CPM
As redes CPM (Critical Path Method) associam as tarefas a grafos. Habitualmente, os nós dos grafos correspondem às tarefas e as arestas a ligações entre elas.
Estas redes podem ser usadas como uma ferramenta de cálculo manual que permite a obtenção do caminho crítico, de datas de início e fim e de margens de tarefas. Os resultados obtidos a partir do cálculo de redes CPM permitem a representação de diagramas de Gantt ou de diagramas de recursos.
A leitura deste tipo de redes não é tão intuitiva como a de diagramas de Gantt. A simples leitura gráfica da rede não permite, por exemplo, conhecer as tarefas de maior duração nem mesmo quais as que iniciam em primeiro lugar, dado que a posição dos nós dos grafos não está necessariamente associada a este critério.
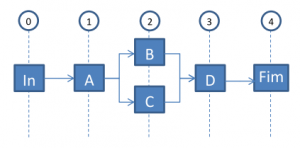
Representação de Redes CPM
Níveis e Tarefas Fictícias Início e Fim
Sugere-se que as redes CPM sejam desenhadas após a determinação dos níveis das respectivas tarefas.
Uma tarefa diz-se de "nível 1" caso não tenha antecessoras, de "nível 2" caso todas as antecessoras sejam de "nível 1" ou será de "nível n" caso todas as antecessoras sejam, no máximo, de "nível n-1".
A cada um destes níveis deverá corresponder um alinhamento para a representação das respectivas tarefas, conforme a imagem apresentada neste ponto.
Sugere-se ainda a representação de duas tarefas fictícias, Início ("In") e "Fim", respectivamente antecessora e sucessora de todas as outras tarefas.
Tarefas
As redes CPM podem ser representadas de diferentes formas. Ilustra-se na figura um conjunto de regras para a representação de tarefas em redes CPM com actividades nos nós do grafo.
Legenda:
- X - Designação da tarefa
- t - Duração
- DIMC – data de início mais cedo
- DFMT – data de fim mais tarde
- DFMC – data de fim mais cedo
- DIMT – data de início mais tarde
- DFMC = DIMC + t
- DIMT = DFMT – t
Se DFMC ≠ DFMT – a actividade tem margens ou folgas não nulas
Se DIMC ≠ DIMT – idem
Metodologia (critérios)
Linha de Balanço
Earned Value Management
Last Planner System
Ferramentas Informáticas
Exemplo de aplicação: MS Project 2003